TUGAS MANDIRI 3 - MATEMATIKA DISKRIT KAMPUS MILENIAL ITBI

 Nama: Geovanni Maruli Tua Sinaga

Kelas: Sore

Jurusan: Sistem informasi

1.3 contoh soal dan penyelesaian tabel kebenaran.

A.Diberikan data:

Pernyataan p bernilai salah
Pernyataan q bernilai benar

Tentukan nilai kebenaran dari konjungsi di bawah ini:
a) p ∧ q
b) p ∧ ~q
c) ~p ∧ q
d) ~p ∧ ~q

Penyelesaian:

Tabel Nilai kebenaran untuk konjungsi :

p	q	p ∧ q
B	B	B
B	S	S
S	B	S
S	S	S

Terlihat bahwa konjungsi bernilai benar jika kedua pernyataan bernilai benar.
Kita terapkan pada soal salah satunya dengan cara tabel:

p	q	~p	~q	p ∧ q	p ∧ ~q	~p ∧ q	~p ∧ ~q
S	B	B	S	S	S	B	S

Dari tabel di atas
a) p ∧ q bernilai salah
b) p ∧ ~q bernilai salah
c) ~p ∧ q bernilai benar
d) ~p ∧ ~q bernilai salah

B.Diberikan nilai dari pernyataan p dan q sebagai berikut:

p	q
B	S

Tentukan nilai kebenaran dari disjungsi berikut:
a) p ∨ q
b) p ∨ ~q
c) ~p ∨ q

Penyelesaian:

Tabel lengkap dari disjungsi sebagai berikut:

.	p	q	p ∨ q
1	B	B	B
2	B	S	B
3	S	B	B
4	S	S	S

Dari data soal dapat diperoleh nilai dari negasi p maupun negasi q, tinggal dibalikkan saja B jadi S, S jadi B

p	q	~p	~q
B	S	S	B

C.(a) Saya melihat harimau di hutan.

(b) Jika saya melihat harimau di hutan, maka saya juga melihat srigala.

Misalkan

p : Amir melihat harimau di hutan

q : Amir melihat srigala

Pernyataan untuk (a): p

Pernyataan untuk (b): p --) q

Tabel kebenaran p dan p --) q 

p |q |p --) q

T |T| T

T| F| F

F| T |T

F |F| T

•Kasus 1: Amir dianggap berbohong, maka apa yang dikatakan Amir itu keduanya

salah ( p salah, q salah)

•Kasus 2: Amir dianggap jujur, maka apa yang dikatakan Amir itu keduanya benar (p

benar, q benar). 

•Tabel menunjukkan bahwa mungkin bagi p dan p --) q benar, tetapi tidak mungkin

keduanya salah. Ini berarti Amir mengatakan yang sejujurnya, dan kita menyimpulkan

bahwa Amir memang benar melihat harimau di hutan.

​ 2.Definisi graf dan unsur–unsur dari graf akan disusun dengan menggunakan bahasa 

himpunan. Karena itu sebelum sampai pada definisi akan dijelaskan syarat dari 

suatu himpunan. Dalam pengertian himpunan disyaratkan bahwa setiap 

elemennya hanya muncul satu kali saja.

Contohnya:

Jenis-jenis graph

Pendahuluan:

Istilah 'gelang pada' graf adalah, sisi yang menghubungkan suatu titik/vertex dengan dirinya sendiri.

Contoh graf yang memiliki gelang:

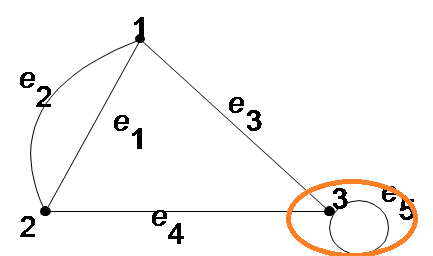
Istilah 'sisi ganda' pada graf ditujukan kepada graf yang memiliki lebih dari satu sisi yang menghubungkan dua buah titik.  

Contoh graf yang memiliki sisi ganda:

 Jenis Graf berdasarkan karakteristik

Graf memiliki karakteristik berdasarkan hal-hal berikut :

1. Keberadaan gelang dan sisi ganda pada graf,
2. Keberhinggaan jumlah sisi pada graf, dan
3. keberadaan orientasi arah.

Jenis	Sisi	Sisi ganda dibolehkan	Sisi gelang dibolehkan
Graf Sederhana (Simple Graf)	tak-berarah	tidak	tidak
Graf Ganda (multi graf)	tak-berarah	Ya	tidak
Graf semu (pseudo graph)	tak-berarah	Ya	Ya
Graf berarah sederhana	Berarah	tidak	tidak
Graf berarah ganda	Berarah	Ya	Ya
Graf Campuran	Berarah dan tak-berarah	Ya	Ya

Graf sederhana (simple graph) :

     Tidak memiliki orientasi arah,

     Tidak memiliki gelang

     Tidak memiliki sisi ganda

Graf ganda (multi graph):

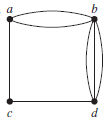
Graf semu (pseudo graph):

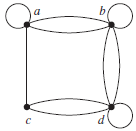
Graf berarah sederhana (directed graph) :

Graf berarah ganda (multi directed graph) :

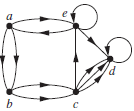
Graf Campuran

$\begin{array}{|c|c|c|c|c|c|} \hline p & q & \neg q & \neg p & p \implies q & \neg q \implies \neg p \\\\ \hline B & B & S & S & B & B \\\\ \hline B & S & B & S & S & S \\\\ \hline S & B & S & B & B & B \\\\ \hline S & S & B & B$

$\begin{array}{|c|c|c|c|c|c|} \hline p & q & \neg q & \neg p & p \implies q & \neg q \implies \neg p \\\\ \hline B & B & S & S & B & B \\\\ \hline B & S & B & S & S & S \\\\ \hline S & B & S & B & B & B \\\\ \hline S & S & B & B &$